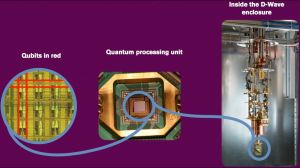
QPU

A Quantum Processing Unit (QPU), also known as a quantum processor, is the core hardware component of a quantum computer that manipulates qubits using the principles of quantum mechanics to perform computations that are intractable for classical processors. Unlike classical CPUs that process bits in binary states (0 or 1), QPUs leverage quantum phenomena such as superposition and entanglement to process qubits that can exist in multiple states simultaneously, enabling exponential scaling of computational power for specific problems.

QPUs are designed to solve complex problems in cryptography, molecular simulation, optimization, and machine learning that would require impractical amounts of time on even the most powerful supercomputers. As of 2025, the field has achieved critical breakthroughs including Google's demonstration of below-threshold quantum error correction with their Willow processor and IBM's roadmap to 200 error-corrected logical qubits by 2029.

Overview

The QPU represents the quantum analog to the classical CPU, serving as the computational heart of quantum computers. However, this analogy can be misleading—QPUs are more accurately described as specialized co-processors similar to GPUs or TPUs, designed to accelerate specific computational tasks rather than serve as general-purpose processors.

A QPU operates by manipulating qubits through quantum logic gates and interactions, forming quantum circuits analogous to classical logic circuits. While classical processors execute operations sequentially or in limited parallelism, QPUs can explore an exponentially large computational space simultaneously—N qubits can represent 2^N states at once, compared to N bits representing only one of 2^N possible states.

Modern quantum computers integrate the QPU within complex systems including:

• Quantum chip: Physical substrate containing qubits and control elements
• Control electronics: Generates precisely timed microwave or laser pulses
• Cryogenic systems: Dilution refrigerators maintaining temperatures near absolute zero (10-15 millikelvin) for superconducting QPUs
• Classical processors: Handle compilation, error correction, and result processing
• Shielding: Electromagnetic and vibrational isolation protecting fragile quantum states

History

Theoretical Foundations (1980-1985)

The theoretical foundations of quantum computing emerged in the early 1980s. Paul Benioff proposed quantum mechanical models of computation in 1980, describing a quantum mechanical Turing machine. Richard Feynman formalized the concept in his 1981 MIT keynote "Simulating Physics with Computers," arguing that quantum computers would be necessary to efficiently simulate quantum systems, and published these ideas in 1982. David Deutsch provided the theoretical framework for universal quantum computers in 1985, establishing that quantum systems could efficiently simulate any physical process.

Early Implementations (1990s)

The 1990s transformed quantum computing from theoretical concept to experimental reality:

• 1994: Peter Shor developed Shor's algorithm for integer factorization, demonstrating exponential quantum speedup for breaking RSA encryption
• 1995: Dave Wineland and Christopher Monroe demonstrated the first two-qubit quantum circuit at NIST
• 1996: Lov Grover developed Grover's algorithm providing quadratic speedup for unstructured search
• 1998: IBM researchers executed Grover's algorithm on a 2-qubit NMR quantum computer
• 1999: NEC demonstrated superconducting qubits using Josephson junctions, establishing the foundation for modern superconducting QPUs

Commercial Development (2000s-2010s)

Development of Commercial Quantum Processors

Year	Company/Institution	Achievement	Significance
2007	D-Wave Systems	28-qubit quantum annealer demonstration	First commercial quantum computing company
2011	D-Wave Systems	D-Wave One (128 qubits)	First commercial QPU sold to Lockheed Martin for ~$10 million
2013	Google/NASA	D-Wave Two (512 qubits)	Established Quantum AI Lab
2016	IBM	5-qubit cloud access	First public cloud quantum computing service
2017	IBM/Intel	~50-qubit processors	Approaching quantum supremacy threshold
2019	Google	Sycamore (53 qubits)	Claimed quantum supremacy - 200 seconds vs 10,000 years classical

Modern Era (2020s)

The 2020s have witnessed rapid acceleration in QPU development:

• 2021: IBM's Eagle processor achieved 127 qubits, surpassing 100-qubit barrier
• 2022: IBM Osprey reached 433 qubits; Xanadu demonstrated photonic quantum advantage with Borealis
• 2023: IBM Condor achieved 1,121 qubits; Atom Computing demonstrated 1,180 neutral atom qubits
• 2024: Google's Willow achieved below-threshold error correction; Quantinuum reached 99.914% two-qubit fidelity
• 2025: Microsoft unveiled Majorana 1 topological qubit prototype (8 qubits); Google reported Quantum Echoes, a verification technique that enabled a ~13,000× speed-up for a molecular-structure task

Fundamental Principles

QPUs derive their computational power from three core quantum mechanical phenomena that have no classical analog:

Superposition

Quantum superposition allows qubits to exist in a probabilistic combination of both |0⟩ and |1⟩ states simultaneously, described mathematically as:

$|\psi \rangle =\alpha |0\rangle +\beta |1\rangle$

where α and β are complex probability amplitudes satisfying |α|² + |β|² = 1.

This enables N qubits to represent all 2^N possible states simultaneously, providing exponential scaling unachievable classically. For perspective, 300 qubits can theoretically process more states than there are atoms in the observable universe.

Entanglement

Quantum entanglement creates correlations between qubits where the quantum state of one qubit cannot be described independently of others. A classic example is the Bell state:

$|\Phi ^{+}\rangle ={\frac {1}{\sqrt {2}}}(|00\rangle +|11\rangle )$

Entangled qubits exhibit perfect correlations regardless of physical separation—measuring one instantly determines the state of others, enabling quantum algorithms to process information in ways impossible classically.

Interference

Quantum interference manipulates probability amplitudes to constructively amplify correct answers while destructively canceling incorrect ones. Quantum algorithms carefully orchestrate interference patterns so that paths leading to wrong answers cancel out while correct solutions reinforce, dramatically increasing the probability of measuring the desired result.

Physical Implementations

Multiple competing technologies exist for implementing QPUs, each with distinct advantages and challenges:

Comparison of Leading Qubit Technologies

Comparison of Major QPU Technologies

Feature	Superconducting	Trapped-Ion	Photonic	Neutral-Atom	Topological
Physical Qubit	Josephson junction circuit	Trapped ion (e.g., Yb+)	Photon properties	Neutral atom in optical trap	Majorana zero modes
Operating Temp	~15 mK	Room temp (trap)	Room temperature	Room temp (trap)	~10 mK
Coherence Time	30-300 μs	Seconds to minutes	Limited by loss	~1 second	Theoretical projection
Gate Speed	10-100 ns	10-100 μs	<1 ns	0.1-1 μs	Unknown
Two-Qubit Fidelity	~99.6-99.7% (best systems)	>99.9%	High (probabilistic)	~99.5%	Theoretical projection
Connectivity	Nearest-neighbor	All-to-all	Reconfigurable	Flexible via Rydberg	Unknown
Scalability	High (chip fab)	Moderate (modular)	Very high (photonics)	High (optical arrays)	Potentially highest
Key Advantages	Fast, manufacturable	High fidelity, long coherence	Room temp, networkable	Scalable, reconfigurable	Theoretical error protection
Main Challenges	Short coherence, cooling	Slow gates, scaling	Probabilistic gates	Atom loss	Unproven at scale
Leading Companies	IBM, Google, Rigetti	IonQ, Quantinuum	PsiQuantum, Xanadu	QuEra, Pasqal, Atom Computing	Microsoft

Superconducting QPUs

Superconducting QPUs dominate current commercial systems, using microscopic circuits with Josephson junctions cooled to near absolute zero where they exhibit quantum behavior.

• Advantages: Fast gate operations (10-100 ns), leverages semiconductor fabrication, demonstrated scaling to >1,000 qubits
• Challenges: Short coherence times (30-300 μs), requires extreme cooling, crosstalk between qubits
• Notable Systems: IBM Condor (1,121 qubits), Google Willow (105 qubits with 99.67% two-qubit fidelity), Rigetti Ankaa-3 (84 qubits)

Trapped-Ion QPUs

Trapped-ion systems suspend individual charged atoms in electromagnetic fields, manipulating them with precision lasers.

• Advantages: Exceptional coherence (seconds to minutes), highest gate fidelities (>99.9%), all-to-all connectivity
• Challenges: Slower gates (10-100 μs), complex scaling beyond 50-100 ions
• Notable Systems: IonQ Forte (36 qubits, #AQ 35), Quantinuum H2 (56 qubits with quantum volume of 8,388,608)

Photonic QPUs

Photonic processors encode quantum information in properties of light particles (photons).

• Advantages: Room temperature operation, minimal decoherence, compatible with fiber networks
• Challenges: Difficult two-qubit gates, photon loss, probabilistic operations
• Notable Systems: Xanadu Borealis (216 modes), PsiQuantum Omega (in development)

Neutral-Atom QPUs

This approach uses arrays of neutral atoms trapped by focused laser beams ("optical tweezers").

• Advantages: High scalability (>1,000 qubits demonstrated), flexible connectivity, long coherence
• Challenges: Atom loss during computation, moderate gate speeds
• Notable Systems: Atom Computing (1,180 qubits), QuEra Aquila (256 qubits)

Topological QPUs

Microsoft's approach uses exotic quasiparticles called Majorana zero modes in specially engineered materials.

• Advantages: Theoretical intrinsic error protection, potential for million-qubit chips
• Challenges: Unproven at scale, limited experimental validation
• Notable Systems: Microsoft Majorana 1 (8-qubit prototype, early stage)

Architecture and Operation

System Components

Modern QPUs integrate multiple subsystems working in concert:

QPU System Architecture

Component	Function	Key Requirements
Quantum Chip	Houses physical qubits and coupling elements	Isolation from noise, precise fabrication
Control Electronics	Generates/delivers gate pulses	Sub-nanosecond timing, low noise
Readout System	Measures qubit states	>99% fidelity, quantum non-demolition
Cryogenic Infrastructure	Maintains operating temperature	10-15 mK for superconducting
Classical Processing	Compilation, error correction, control	Real-time processing, low latency
Shielding	Protects from environmental noise	Electromagnetic, vibrational, thermal

Operational Workflow

The execution of a quantum algorithm follows these steps:

1. Compilation: Classical compiler translates high-level algorithm into hardware-specific quantum circuits
2. Initialization: All qubits prepared in known state (typically |0⟩)
3. Gate Sequence: Control pulses apply quantum gates according to compiled circuit
4. Measurement: Qubit states collapsed and read out as classical bits
5. Repetition: Process repeated thousands of times to build probability distribution
6. Post-processing: Classical analysis extracts final answer from measurement statistics

Quantum Gates

Quantum logic gates manipulate qubit states through controlled interactions:

• Single-qubit gates: Rotations around Bloch sphere axes (X, Y, Z rotations, Hadamard)
• Two-qubit gates: Create entanglement (CNOT, CZ, iSWAP)
• Gate implementation: Microwave pulses (superconducting), laser pulses (trapped ion/neutral atom)
• Fidelity requirements: >99.9% for practical error correction

Performance Metrics

Quantum Volume

Quantum volume combines multiple performance aspects into a single metric:

• Accounts for qubit count, connectivity, gate fidelity, and measurement accuracy
• Higher values indicate better overall system performance
• Record: Quantinuum H2 achieved quantum volume of 8,388,608 (2^23) in 2023

Key Performance Indicators

Metric	Description	Current State-of-Art (2025)	Target for Fault Tolerance
Qubit Count	Number of physical qubits	1,000-5,000	1-10 million
Coherence Time (T1, T2)	Qubit lifetime	30-300 μs (superconducting) Seconds (trapped ion)	Application dependent
Single-Qubit Fidelity	Single gate accuracy	99.95-99.998%	>99.99%
Two-Qubit Fidelity	Entangling gate accuracy	99.5-99.914%	>99.9%
Readout Fidelity	Measurement accuracy	99-99.5%	>99.9%
CLOPS	Circuit Layer Operations/Second	150,000 (IBM)	>1 million
Logical Qubit Error Rate	After error correction	10^-3 to 10^-6	<10^-10

Applications

QPUs excel at problems with inherent quantum structure or exponential classical complexity:

Quantum Simulation

• Drug Discovery: Simulating molecular interactions, protein folding, drug-target binding
• Materials Science: Designing catalysts, batteries, superconductors
• Example: In 2025, Google reported Quantum Echoes, a verification technique that enabled a ~13,000× speed-up for a molecular-structure task, with a method for certifying the result's correctness

Optimization

• Finance: Portfolio optimization, risk analysis, derivative pricing
• Logistics: Route optimization, supply chain, scheduling
• Manufacturing: Process optimization, quality control
• Example: JPMorgan researchers demonstrated certified quantum randomness on Quantinuum hardware; certified randomness is useful for Monte Carlo methods in finance

Cryptography

• Code Breaking: Shor's algorithm threatens current RSA/ECC encryption
• Quantum Security: Quantum key distribution for unbreakable communication
• Resource Requirements: Breaking RSA-2048 with Shor's algorithm would require thousands of logical qubits; one influential analysis suggests ~20 million noisy physical qubits (under specific assumptions) would be needed to factor RSA-2048 in ~8 hours, underscoring that calendar timelines remain speculative

Machine Learning

• Quantum Machine Learning: Enhanced feature spaces, quantum neural networks
• Speedups: HHL algorithm for linear systems, quantum kernel methods
• Applications: Pattern recognition, optimization, data analysis

Challenges and Limitations

Decoherence and Error Rates

• Decoherence: Quantum states decay in microseconds to seconds depending on technology
• Error accumulation: Current error rates of 0.1-1% per gate limit circuit depth
• Environmental sensitivity: Vibrations, electromagnetic fields, cosmic rays cause errors
• Mitigation strategies: Error correction codes, improved materials, better isolation

Quantum Error Correction

Quantum error correction enables fault-tolerant computation but requires massive overhead:

• Physical-to-logical ratio: 1,000-10,000 physical qubits per logical qubit with current error rates
• Surface code: Leading approach arranges qubits in 2D grid for error detection/correction
• Breakthrough: Google's Willow achieved below-threshold correction—errors decrease as more qubits added
• Alternative codes: Quantum LDPC codes promise 10× efficiency improvement

Scalability Challenges

• Wiring complexity: Each qubit needs control/readout lines
• Cooling limits: Dilution refrigerators struggle beyond 10,000 qubits
• Control electronics: Classical processing requirements scale with qubit count
• Solutions: Modular architectures, cryogenic electronics, photonic interconnects

Current State and Future Outlook

NISQ Era (2025-2029)

The current Noisy Intermediate-Scale Quantum (NISQ) era features:

• 50-1,000 noisy physical qubits
• Limited to ~1,000 gate operations before decoherence
• Specialized quantum advantages on narrow problems
• Hybrid quantum-classical algorithms (VQE, QAOA) showing practical value

Path to Fault Tolerance (2029-2035)

Industry roadmaps converge on achieving practical fault-tolerant systems:

Major QPU Development Roadmaps

Company	2025 Status	2029 Target	2035 Vision
IBM	156-qubit Heron R2	200 logical qubits (Starling)	2,000+ logical qubits
Google	105-qubit Willow	"Useful error-corrected QC"	Million physical qubits
IonQ	36 qubits (#AQ 35)	#AQ 64+ systems	Scalable trapped-ion architectures
Microsoft	8-qubit Majorana 1 (prototype)	Scalable topological qubits	Million qubits/chip (theoretical)
Quantinuum	56 qubits (QV 8,388,608)	Advancing toward fault tolerance	Commercial quantum advantage

Market Projections

• Current market: ~$1 billion annually (2025)
• 2030 projection: $5-15 billion (conservative) to $45-72 billion (optimistic)
• Key drivers: Drug discovery, materials science, financial modeling, logistics optimization

See Also

• Quantum computing
• Qubit
• Quantum algorithm
• Quantum error correction
• Quantum supremacy
• Quantum machine learning
• Dilution refrigerator
• Post-quantum cryptography